Difference between revisions of "EMO:How EMO models SFT constraints"
| Line 16: | Line 16: | ||
The power flows used in this relationship are from and AC power flow model, which will be constructed using the SPD solution in conjunction with reactive power modelling and a detailed model of the transmission grid componentry. The full information for creating this AC model is not available to us, so there is inevitable degree of approximation in estimating SFT constraints from our point of view. | The power flows used in this relationship are from and AC power flow model, which will be constructed using the SPD solution in conjunction with reactive power modelling and a detailed model of the transmission grid componentry. The full information for creating this AC model is not available to us, so there is inevitable degree of approximation in estimating SFT constraints from our point of view. | ||
To model this constraint in EMO we also need to estimate the nature of the pre/post power flow constraint as much as it relates to the SPD solution. We do not currently have access to the definitions of these functions, but we are informed that they are quadratic functions and they will pass through the point (C, C) where C is the thermal capacity of the line, which is a value we do have access to. | To model this constraint in EMO we also need to estimate the nature of the pre/post power flow constraint as much as it relates to the SPD solution. We do not currently have access to the definitions of these functions, but we are informed that they are quadratic functions and they will pass through the point (C, C) where C is the thermal capacity of the line, which is a value we do have access to. | ||
| − | The slope of the curve is given explicitly in the resulting constraint equation in SPD, being negative the value A in Equation 1. | + | The slope of the curve is given explicitly in the resulting constraint equation in SPD, being negative the value A in Equation 1. |
| + | We can also the arc flows from the SPD solution so, given enough instances of an SFT equation for a particular protected line, we might be able to estimate its pre/post constraint curve. We are informed that the thermal environment used for each curve is purely dependent on the Summer/Shoulder/Winter designation of the trading period so we can make a sample of all the constraints that fall into each category. | ||
| + | |||
At this point however there is no significant correlation observable between the tangent slope of the SFT constraints (A in Equation 1) and the power flows in the solution. What correlation there is appear to be overshadowed by the variability in the limit, which is sometimes seen to fall below the (C, C) point, probably due to the effects of reactive power flows. For these reasons the best fit for α and β are currently calculated by setting α to 0 and β to the average slope A. | At this point however there is no significant correlation observable between the tangent slope of the SFT constraints (A in Equation 1) and the power flows in the solution. What correlation there is appear to be overshadowed by the variability in the limit, which is sometimes seen to fall below the (C, C) point, probably due to the effects of reactive power flows. For these reasons the best fit for α and β are currently calculated by setting α to 0 and β to the average slope A. | ||
| Line 22: | Line 24: | ||
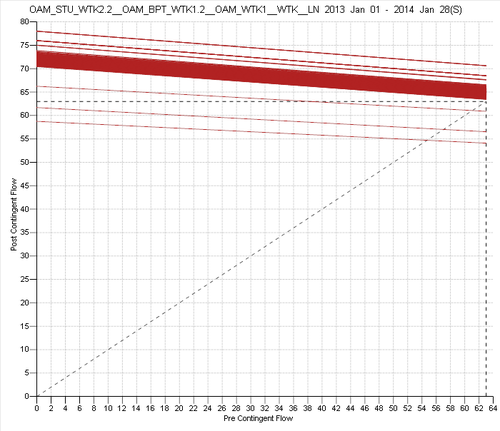
Some examples of constraint variation are shown in the figures below: | Some examples of constraint variation are shown in the figures below: | ||
| − | Figure 1: Summer SFT constraints on the NSY_ROX.1 line (contingent line CYD_TWZ1.1)[[File: | + | [[File:Graph_SFT_1.PNG|500px|thumb|right|Figure 1: Summer SFT constraints on the NSY_ROX.1 line (contingent line CYD_TWZ1.1)]] |
| − | + | [[File:Graph_SFT_2.PNG|500px|thumb|right|Figure 2: Summer SFT constraints on the OAM_STU_WTK2.2 line (contingent line OAM_BPT_WTK1.2)]] | |
| − | + | [[File:Graph_SFT_3.PNG|500px|thumb|right|Figure 3: Winter SFT constraints on the ARI_KIN1.1 line (contingent line ARI_KIN2.1)]] | |
| − | |||
Revision as of 16:29, 28 January 2014
Automatic SFT constraint generation in EMO
The aim of automatic SFT constraint modelling in EMO is to model the SFT constraints that are generated as part of the dispatch and pricing solution in SPD. These constraints are designed to avoid thermal overloading of a line in the event of the unexpected outage of any other line. SFT constraints appear in the dispatch and pricing optimisation model as linear constraints between two lines. For example:
-0.902*OHK_WRK.1+1.274*THI_WKM1.1 <= 605.79
In this case THI_WKM1.1 is the line being protected from overload and OHK_WRK.1 is the line which may cause overload in THI_WKM1.1 if it has an outage. The general form of the SFT constraint is
Equation 1. \(A F_{m} + B F_{c} \leq C\)
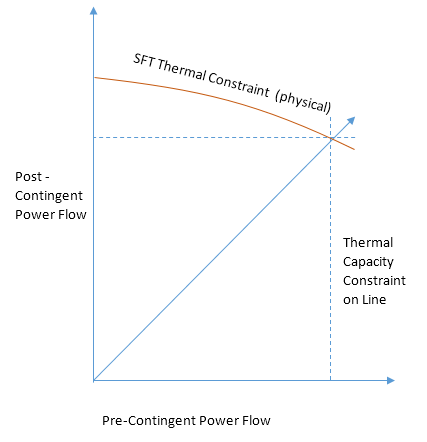
Where \(F_{m}\) is the flow on the protected line and \(F_{c}\) is the flow on the contingent line. The physical nature of the SFT constraint depends on various characteristics of the line being protected, the thermal environment and the mitigating measures available if an outage occurs. The constraint can be expressed as a function of the loading on the line before an outage occurs (pre-contingent) and the loading after an outage occurs (post-contingent). The higher the line is loaded pre-contingency the greater its expected temperature, giving it less capacity to absorb extra power in the event of a contingency
The physical SFT constraint is shown in the diagram 1. This constraint will depend on the thermal environment
In SPD the constraint above is modelled as a linear constraint which represents a tangent of the physical constraint at the point where the pre-contingent power flow matches the power flow in the solution of SPD. Because the constraint may affect dispatch this is an iterative process, the resulting constraint is shown in diagram 2.
The power flows used in this relationship are from and AC power flow model, which will be constructed using the SPD solution in conjunction with reactive power modelling and a detailed model of the transmission grid componentry. The full information for creating this AC model is not available to us, so there is inevitable degree of approximation in estimating SFT constraints from our point of view. To model this constraint in EMO we also need to estimate the nature of the pre/post power flow constraint as much as it relates to the SPD solution. We do not currently have access to the definitions of these functions, but we are informed that they are quadratic functions and they will pass through the point (C, C) where C is the thermal capacity of the line, which is a value we do have access to. The slope of the curve is given explicitly in the resulting constraint equation in SPD, being negative the value A in Equation 1. We can also the arc flows from the SPD solution so, given enough instances of an SFT equation for a particular protected line, we might be able to estimate its pre/post constraint curve. We are informed that the thermal environment used for each curve is purely dependent on the Summer/Shoulder/Winter designation of the trading period so we can make a sample of all the constraints that fall into each category.
At this point however there is no significant correlation observable between the tangent slope of the SFT constraints (A in Equation 1) and the power flows in the solution. What correlation there is appear to be overshadowed by the variability in the limit, which is sometimes seen to fall below the (C, C) point, probably due to the effects of reactive power flows. For these reasons the best fit for α and β are currently calculated by setting α to 0 and β to the average slope A.
These values are delivered to EMarketOffer using the AverageLineProtectionFactors<date>.csv file in the <EMO Data Dir>/Inputs/Grid/SFT directory. Lines for which we have no data have these values set to 0 and 1.04, which is the average protection value for lines which are not under enhanced protection schemes.
Some examples of constraint variation are shown in the figures below:
To estimate the curve then we can try to find the linear relationship between the slope and the pre-contingent flow. What we are looking for in the equations we are seeing in SPD is two values, call them α, β, for which the following relationships exist over all instances of a particular combination of SFT constraint and thermal environment
Equation 2. \(C \simeq \alpha \underline{F}_{m}+\beta\)
Equation 3. \(C \simeq C+ \frac{ \alpha }{2} \big(C- \underline{F}_{m} \big)^{2}\)